安卓逆向-Des算法详解

DES算法详解

1. 简介

• DES（Data Encryption Standard，数据加密标准）是一种对称加密算法，由IBM在20世纪70年代初期研发，并在1977年被美国国家标准局（现为NIST）采纳为联邦信息处理标准；
• 总的来说，DES加密的过程就是通过一系列置换、异或、扩展等运算，将明文分成若干个小块，然后根据主密钥生成一系列的轮密钥，利用轮密钥对每个小块进行加密，最终将加密结果重新组合成一个整体，得到密文；
• DES 的功能是：给定一个 64 位的明文和一个 64 位的密钥，输出一个 64 位的密文，这个密文可以用相同的密钥解密；所谓“64位的密钥”，其实里面只有54位在起作用；剩余的位可以直接丢弃，或者当作奇偶校验位；
• 虽然 DES 一次只能加密 8 个字节，但我们只需要把明文划分成每 8 个字节一组的块，就可以实现任意长度明文的加密；如果明文长度不是 8 个字节的倍数，还得进行填充；现在流行的填充方式是 PKCS7 / PKCS5，都是很简单的思路，用于把任意长度的文本填充成 8 字节的倍数长，也能方便地恢复原文，这里不再赘述；
• 此外，独立地对每个块加密，最后直接拼起来是不行的（这种方式称为“电子密码本”，ECB 模式；它会导致明文中重复的块，加密结果也重复，这对于图片之类的数据来说几乎是致命的）；

• 分组相关信息：

  • 输入：64比特(8个字节、16个16进制数)；
  • key： 64比特(8个字节、16个16进制数)；
  • 结果：64比特(8个字节、16个16进制数)；
• DES的key必须是8个字节；

2. 流程图

• 算法的流程图如下：

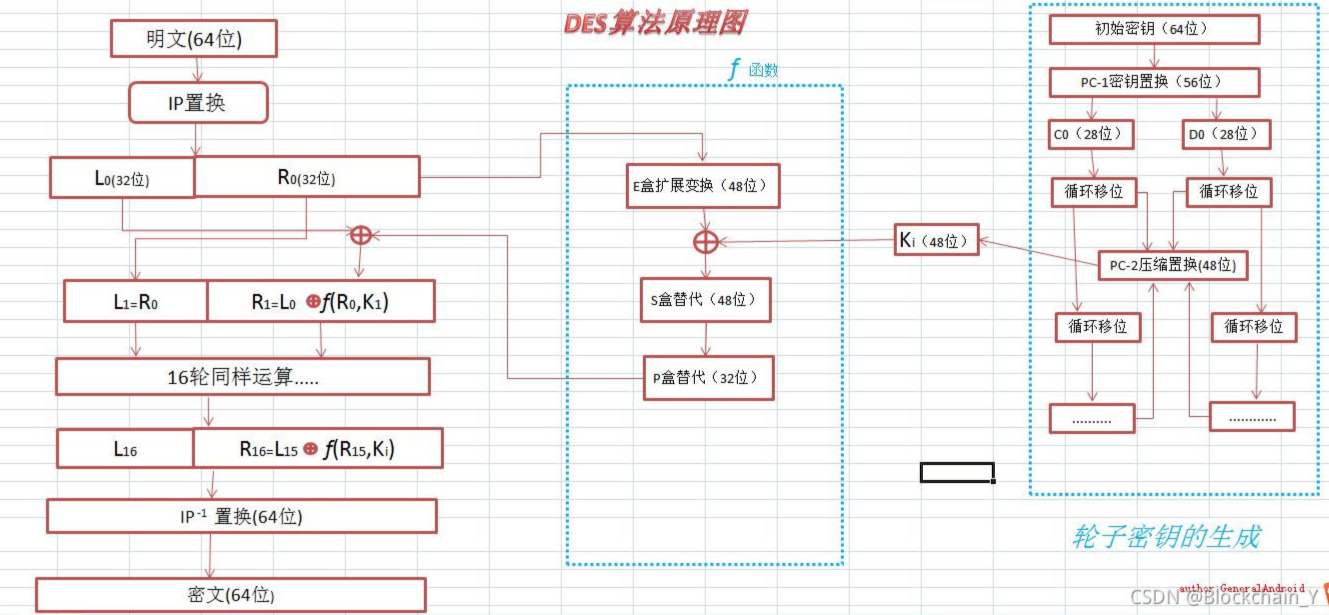
• 关于其中一些术语的解释：

  • IP表：明文初始置换
  • IP-1表：明文结束置换
  • PC-1表：Key初始置换
  • PC-2表：K0-K16置换
  • E表：扩展Rn-1与Kn进行异或

3. 算法流程

• 还可以参考：https://www.yuque.com/nanren-w8l2z/xgu63m/owxzxq7qn0b5o53x
• DES分两部分：明文的处理以及密钥的编排二进制流处理，这里以下方的例子来描述整个算法：

输入：0123456789abcdef (hex)
key：133457799bbcdff1(hex)
输出：85e813540f0ab405 (hex)
模式: ECB

3.1 密钥编排

• 首先，密钥的二进制表现形式为（64位）：

00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001

• 接下来，经过PC1表(置换选择表1)重新排列，这里的结果是56位的，也就是说，最开始传进来的秘钥⼀共64位，但是马上就会经过一轮置换去掉8位，只有56位会被使用；
• PC1表如下：

PC_1 = [57, 49, 41, 33, 25, 17, 9,
        1, 58, 50, 42, 34, 26, 18,
        10, 2, 59, 51, 43, 35, 27,
        19, 11, 3, 60, 52, 44, 36,
        63, 55, 47, 39, 31, 23, 15,
        7, 62, 54, 46, 38, 30, 22,
        14, 6, 61, 53, 45, 37, 29,
        21, 13, 5, 28, 20, 12, 4]
# 长度：56

• 它的置换规则非常简单，就是按照PC1表，将密钥的二进制的第57位，放在第一位，将49位放在第二位，以此类推，其中没有 8，16，24，32，40，48，56，64；注意，这里索引是1开始，没记错的话只有S盒替换是从0开始的；
• 也就意味着以下是等效的 DES多个Key对应同一个加密结果：

00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001
等效
0001001 0011010 0101011 0111100 1001101 1011110 1101111 1111000

0001001* 0011010* 0101011* 0111100* 1001101* 1011110* 1101111* 1111000*

• 注：数的时候从1开始不是0, 看PC表的顺序为从左到右然后从上至下 ；
• 置换后的结果为（56位）：

1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111

• 随后，将这56比特长的密钥分成左右两部分，这里称为Left0和Right0(只拆分一次)；

Left0:  1111000 0110011 0010101 0101111
Right0: 0101010 1011001 1001111 0001111  

• 然后进行循环左移，进行⼀共16轮运算（SHIFT数组共16位）；

SHIFT = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
# 长度：16

• L1: 对Left0循环左移1位，左移位数 = SHIFT[0] = 1 得到；

1110000 1100110 0101010 1011111

• R1 : 对Right0循环左移1位，左移位数 = SHIFT[0] = 1 得到；

1010101 0110011 0011110 0011110 

• 然后进行拼接 L1 + R1（56位）；

1110000 1100110 0101010 1011111 1010101 0110011 0011110 0011110

• 拼接完成之后，使用PC2表(置换选择表2)进行置换；规则和PC1表一样，这里索引是1开始；

PC_2 = [14, 17, 11, 24, 1, 5, 3, 28,
        15, 6, 21, 10, 23, 19, 12, 4,
        26, 8, 16, 7, 27, 20, 13, 2,
        41, 52, 31, 37, 47, 55, 30, 40,
        51, 45, 33, 48, 44, 49, 39, 56,
        34, 53, 46, 42, 50, 36, 29, 32]
# 长度：48

• L1R1经过置PC_2置换后的结果为48位，这里的L1R1指的是它们拼接；
• 此时得到的结果是第⼀个子密钥K1；

K1：00011011 00000010 11101111 11111100 01110000 01110010

• L2：对L1进行循环左移SHIFT[1]位；

110000 1100110 0101010 10111111

• R2：对R1进行循环左移SHIFT[1]位；

010101 0110011 0011110 00111101

• 然后进行拼接 L2 + R2（56位）；

110000 1100110 0101010 10111111 010101 0110011 0011110 00111101

• L2R2经过置PC_2置换后的结果为48位；此时得到的结果是第二个子密钥K2；

K2：01111001 10101110 11011001 11011011 11001001 11100101

• 剩下的就是以此类推，直到生成K16，16轮的子密钥；
• 需要注意，实际上加密用的会是生成的这16组子密钥，也就是K1-K16，主密钥则不参与加密运算；
• 后续使用的时候，哪一轮就对应K几的秘钥；

3.2 明文处理

• 首先，明文的字符串和二进制表示如下：

0123456789abcdef (hex)
00000001 00100011 01000101 01100111 10001001 10101011 11001101 11101111

• 首先根据IP表，对明文进行初始置换，置换的规则也是一样的，这里索引也是1开始；

IP = [58, 50, 42, 34, 26, 18, 10, 2,
      60, 52, 44, 36, 28, 20, 12, 4,
      62, 54, 46, 38, 30, 22, 14, 6,
      64, 56, 48, 40, 32, 24, 16, 8,
      57, 49, 41, 33, 25, 17, 9, 1,
      59, 51, 43, 35, 27, 19, 11, 3,
      61, 53, 45, 37, 29, 21, 13, 5,
      63, 55, 47, 39, 31, 23, 15, 7]
# 长度：64

• 置换后的结果为64位的数据；

11001100 00000000 11001100 11111111 11110000 10101010 11110000 10101010

• 把上一步把重排的结果分两半，这里也称为L0和R0；

L0: 11001100 00000000 11001100 11111111
R0: 11110000 10101010 11110000 10101010  

• 接下来，就会对L0、R0做16轮迭代，计算公式如下：

Ln = Rn-1
Rn = Ln-1 xor f(Rn-1, Kn)

• 比如：

L1：R0 -->>(总是上⼀步的R)；
R1： L0 xor F(R0, K1) -->> (总是上一步的 L 异或 F(R, K) 的结果); F函数会比较复杂

• 这个公式就是16轮迭代的基本套路，下面以 n = 1 为例(这里会有1-16，没有0)：

• 第一步：

  • E(R0)，也就是使用EXPEND表把R0从32位扩展到48位，因为之后要与密钥异或，密钥都是48位的所以要扩充到48位；

  EXPEND = [32, 1, 2, 3, 4, 5,
            4, 5, 6, 7, 8, 9,
            8, 9, 10, 11, 12, 13,
            12, 13, 14, 15, 16, 17,
            16, 17, 18, 19, 20, 21,
            20, 21, 22, 23, 24, 25,
            24, 25, 26, 27, 28, 29,
            28, 29, 30, 31, 32, 1]
  # 长度：48

  • 得到的结果就是48位了；

  01111010 00010101 01010101 01111010 00010101 01010101

• 第二步：

  • E(R0) ^ k，也就是和这一轮的秘钥异或，得到结果（48位）；

  011000 010001 011110 111010 100001 100110 010100 100111

• 第三步：

  • S(E(R0) ^ k)，在S盒中找到对应的位置，这一步稍微复杂一些；
  • 把第二步得到的结果经过 B1B2B3B4B5B6B7B8 此规则分段，那么就会得到这样的8段数据：

  B1: 011000
  B2: 010001
  B3: 011110
  B4: 111010
  B5: 100001
  B6: 100110
  B7: 010100
  B8: 100111

  • 以B1 011000 为例，分成两部分；
  • 第一部分：第一位和最后一位加起来是00，对应的10进制为0，也就是第0行；
  • 第二部分：中间4位为1100，对应的10进制为12列，也就是第12列；
  • 因为是B1，就从S_BOX[0]开始数，从S_BOX第0个索引开始数(0, 12) -> 就是5 转成二进制为0101；
  • S_BOX一共有8组数据，正好对应B1-B8；这里的索引从0开始；

  S_BOX = [
      [[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
       [0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
       [4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
       [15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]],
  
      [[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
       [3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
       [0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
       [13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9]],
  
      [[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
       [13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
       [13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
       [1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12]],
  
      [[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
       [13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
       [10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
       [3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14]],
  
      [[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
       [14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
       [4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
       [11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3]],
  
      [[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
       [10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
       [9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
       [4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13]],
  
      [[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
       [13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
       [1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
       [6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12]],
  
      [[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
       [1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
       [7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
       [2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]]
  ]

  • 最后经过8轮 * 4位，S(E(R0) ^ k) 的结果就变成了32位；

• 第四步：

  • P置换，将S盒后得到的结果经过P表进行置换，重新排列后得到32位；

  P = [16, 7, 20, 21, 29, 12, 28, 17,
       1, 15, 23, 26, 5, 18, 31, 10,
       2, 8, 24, 14, 32, 27, 3, 9,
       19, 13, 30, 6, 22, 11, 4, 25]
  # 长度：32

• 第五步： L0 xor F函数的结果

L1: 11110000 10101010 11110000 10101010
R1: 11101111 01001010 01100101 01000100

• 经过上述步骤周而复始最后得到L16R16，将L16 R16 倒换相加，最后⼀轮才倒换，别的轮次不用；

L16: 01000011 01000010 00110010 00110100
R16: 00001010 01001100 11011001 10010101

• R16 + L16 (64位)，这里注意是倒换过的；

00001010 01001100 11011001 10010101 01000011 01000010 00110010 00110100

• 最后通过IP_1表进行置换得到结果；

IP_1 = [40, 8, 48, 16, 56, 24, 64, 32,
        39, 7, 47, 15, 55, 23, 63, 31,
        38, 6, 46, 14, 54, 22, 62, 30,
        37, 5, 45, 13, 53, 21, 61, 29,
        36, 4, 44, 12, 52, 20, 60, 28,
        35, 3, 43, 11, 51, 19, 59, 27,
        34, 2, 42, 10, 50, 18, 58, 26,
        33, 1, 41, 9, 49, 17, 57, 25]
# 长度：64

• 最终结果就是：85e813540f0ab405；

10000101 11101000 00010011 01010100 00001111 00001010 10110100 00000101

• 在整体的运算里面，只有S盒的运算是从0开始取下标的，其他都是从1开始取的，需要注意；
• 末置换就是初始置换的逆运算，明文经过初始置换，不做任何处理再进行末置换，值等于它自身；可以对比初始置换和末置换的两个数组，比如第一个40，在初始置换的位置其实是1；第二个8在初始置换的位置是2；

4. 其他

• des的魔改点相对较多，其中有很多常量表都可以改，但是可能会影响算法的安全性；
• 另外，明文的初始置换和末置换，去除或者修改，都不影响des算法的安全性，但是结果是会被影响；这个算是一个可以修改的点；
• S_BOX也是可以修改的，但依旧需要注意安全性；
• 关于填充，与aes的一样，并不是des特有的；
• 关于加密模式，也不是des特有的，前面的示例是ecb模式计算的，用的比较多的还有cbc，和ecb相比多了一个IV，加密时，明文首先与IV异或，然后将结果进行块加密，输出密文，同时本次的输出密文作为下一个块加密的IV；
• 关于CBC模式更加朴素的说法是：每个明文分组在加密前多一个步骤，和上一个分组的密文块进行异或运算；因为第一个明文块没有所谓的“上一个分组的密文块“，所以需要人给一个64比特，或者说8字节的输入，我们叫它初始化向量IV；这里的异或位置需要注意，是加密前；
• 关于ECB模式：每个分组之间单独加密，互不影响，他就没有IV了，只有key；
• 关于3des加密算法：

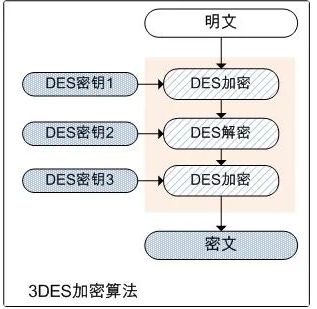
• 3des的秘钥是24个字节，实际上就是3个des秘钥，也就是三次des加密，但是需要注意，第二次是解密；
• 如果三段秘钥是一样的话，3des加密出来的结果其实就和一次des加密的结果是一样的；